2025-08-24 从零构建大模型-徒手组装GPT

发布于 2025年08月24日 • 4 分钟 • 790 字

Table of contents

GPT的几个概念：
一、打好框架：构建Dummy类
二、层归一化
三、GELU函数和前馈神经网络
四、快捷连接
五、Transformer块
六、GPT架构的真正实现
七、GPT将输出张量转为文本
八、了解模型架构及其规模

《从零构建大模型》8周学习计划（按周打卡！） 1️⃣ 数据预处理✅ 2️⃣ 注意力机制✅ 3️⃣ 徒手组装GPT✅ 4️⃣ 徒手训练GPT 5️⃣ 微调：分类 6️⃣ 微调：SFT 7️⃣-8️⃣ 缓冲周

GPT的几个概念：

参数：指模型的可训练权重，本质是模型的内部变量。在训练过程中通过调整和优化来最小化特定的损失函数来学习。
GPT-2和GPT3：架构基本相同，训练的数据量不同，参数量不同。GPT-2的权重公开，GPT-3的权重没有。
GPT2的config vocab_size表示使用50257个token组成的词汇表。

context_length指的是模型一次输入的最大token 数量。

emb_dim表示嵌入维度大小。

n_heads表示多头注意力机制中注意力头的数量。

n_layers表示模型中的Transformer块数量。

drop_rate表示表示有10%的隐藏单元被随机丢弃，以防止过拟合。

qkv_bias指的是是否在多头注意力机制的线性层中添加一个偏置向量，用于查询、键和值的计算。

GPT_CONFIG_124M ={
    "vocab_size":50257,
    "context_length":1024,
    "emb_dim":768,
    "n_heads":12,
    "n_layers":12,
    "drop_rate":0.1,
    "qkv_bias":False
}

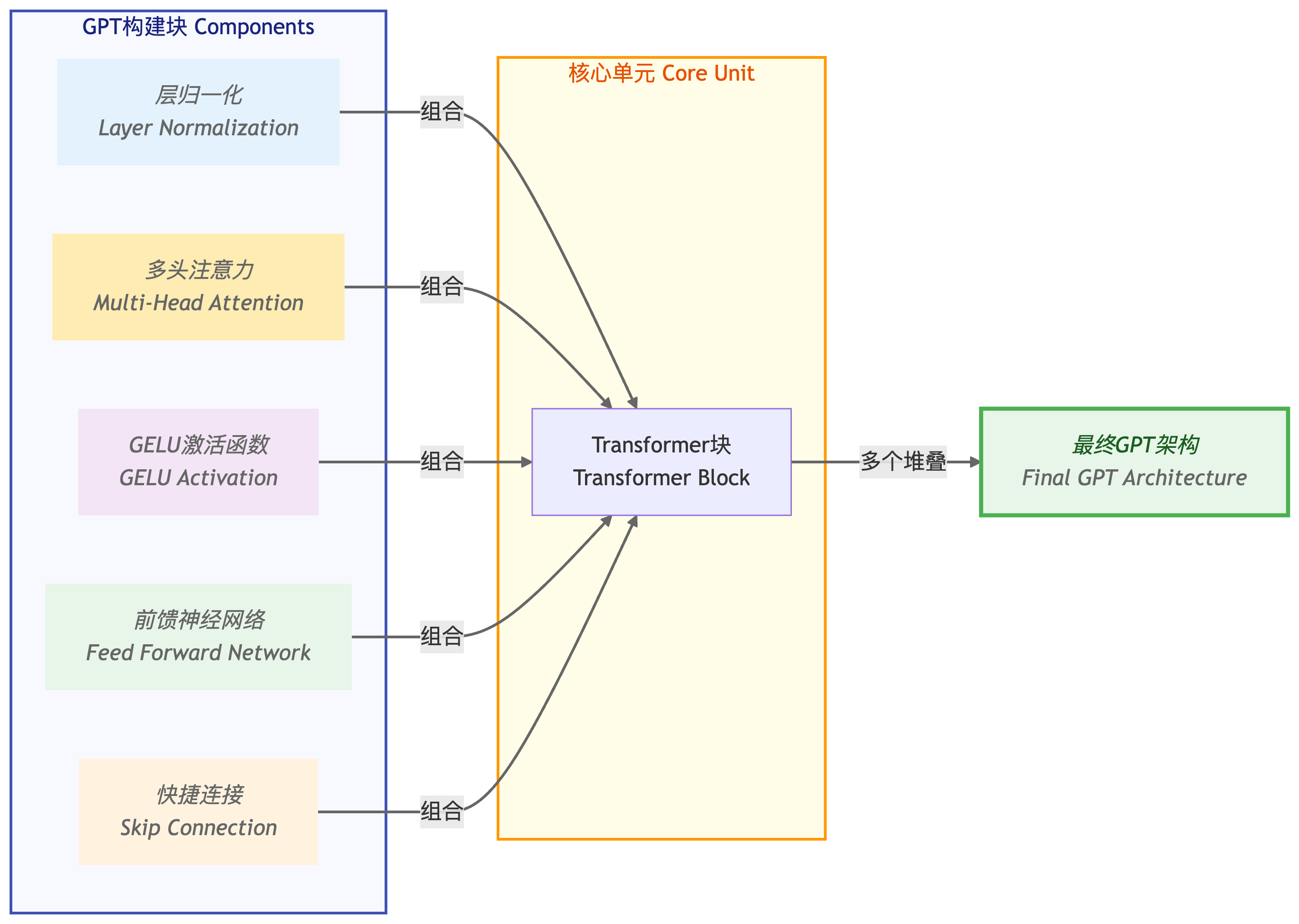
GPT大语言模型的组件：嵌入层、Transformer块、输出层。
Transformer块包括层归一化，GELU激活函数、前馈神经网络、残差链接和多头注意力模块。

一、打好框架：构建Dummy类

这里的Dummy类只用于结构完整性，并不是具体真实的实现。
数据在模型中的处理流程：它首先计算输入索引的词元和位置嵌入，然后应用dropout，接着通过Transformer块处理数据，再应用归一化，最后使用线性输出层生成logits。

代码理解：

nn.Embedding 的本质是创建一个权重矩阵，是把词表里的每一个 token_id 映射成一个向量。
self.tok_emb = nn.Embedding(config[“vocab_size”], config[“emb_dim”])—— 在 init 里建表，告诉模型：词表有多大，每个 token 要映射成多少维的向量。这一步只发生一次，把权重矩阵（形状 [vocab_size, emb_dim]）存到 self.tok_emb 里。
tok_emb = self.tok_emb(in_idx)—— 在 forward 里查表（把输入的 token_id 拿去这张表里查对应的向量）。这一步每次前向传播都会调用，输入是形状 [batch, seq_len] 的整数张量，输出是 [batch, seq_len, emb_dim] 的嵌入张量。

import torch 
import torch.nn as nn

class DummyTransformerBlock(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()
    def forward(self, x):
        return x

class DummyLayerNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-5) -> None:
        super().__init__()
    def forward(self, x):
        return x

class DummyGPTModel(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()
        self.tok_emb = nn.Embedding(config["vocab_size"], config["emb_dim"])
        self.pos_emb = nn.Embedding(config["context_length"], config["emb_dim"])
        self.drop = nn.Dropout(config["drop_rate"])
        self.transformer_blocks = nn.Sequential(*[
            DummyTransformerBlock(config) for _ in range(config["n_layers"])
        ])  # 使用占位符替换TransformerBlock

        self.final_norm = DummyLayerNorm(config["emb_dim"])
        self.out_head = nn.Linear(config["emb_dim"], config["vocab_size"], bias=False)

    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_emb = self.tok_emb(in_idx)
        pos_emb = self.pos_emb(torch.arange(seq_len, device=in_idx.device))
        x = tok_emb + pos_emb
        x = self.drop(x)
        x = self.transformer_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

二、层归一化

层归一化指调整神经网络层的输出，使其均值为0且方差为1。
为什么要层归一化：使训练稳定，加速权重收敛。
什么时候用：多头注意力的前后；最终输出层之前
LayerNorm 沿着列方向（hidden_size）做归一化

代码理解：

变量eps是一个小常数，在归一化过程中会被加到方差上以防止除零错误。
scale和shift是两个可训练的参数（与输入维度相同），训练过程中大语言模型会自动调整

class LayerNorm(nn.Module):
    def __init__(self, emb_dim):
        super().__init__()
        self.eps = 1e-5
        self.scale = nn.Parameter(torch.ones(emb_dim))
        self.shift = nn.Parameter(torch.zeros(emb_dim))
    def forward(self,x):
        mean = x.mean(dim=-1, keepdim=True)
        var = x.var(dim=-1, keepdim=True)
        norm_x = (x - mean) / torch.sqrt(var + self.eps)
        return self.scale * norm_x + self.shift

三、GELU函数和前馈神经网络

GELU(Gaussian Error Linear Unit) 其精确的定义为GELU(x) = x \cdot \Phi(x)，其中\Phi(x)是标准高斯分布的累积分布函数。

GELU的好处：

有平滑性，可以在训练过程中带来更好的优化效果
对负输入会输出一个小的非零值。这意味着在训练过程中，接收到负输入的神经元仍然可以参与学习

class GELU(nn.Module):
    def __init__(self) -> None:
        super().__init__()

    def forward(self,x):
		    # 这个是近似实现
        return 0.5 * x * (1 + torch.tanh(torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3))))

前馈神经网络由两个线性层和一个GELU激活函数组成。

这个网络的输入和输出维度保持一致，但它通过第一个线性层将嵌入维度扩展到了更高的维度（代码这里是4倍输入的维度）。扩展之后，应用非线性GELU激活函数，然后通过第二个线性变换将维度缩回原始大小。这种设计允许模型探索更丰富的表示空间。

为什么是4倍呢？

一是早期 Transformer 论文设置的4倍，后续所有实现为了可复现，就沿用了同一比例。二是4倍在工程上能够平衡容量和计算量，被认为是一个比较好的考虑。


class FeedForward(nn.Module):
    def __init__(self,config):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(config["emb_dim"], 4 * config["emb_dim"]),
            GELU(),
            nn.Linear(4 * config["emb_dim"], config["emb_dim"]),
        )
    def forward(self,x):
        return self.layers(x)

四、快捷连接

快捷连接就是残差连接，这里为了和书上保持一致，就继续用“快捷链接”这个名字了。

快捷连接通过跳过一个或多个层，为梯度在网络中的流动提供了一条可替代且更短的路径。它让梯度可以直接反向传播，有效解决了深层网络中的梯度消失问题。

x’ = x + Attention(LayerNorm(x))

五、Transformer块

Transformer块包括层归一化，GELU激活函数、前馈神经网络、残差链接和多头注意力模块。

当Transformer块处理输入序列时，序列中的每个token都被表示为一个固定大小的向量（此处为768维）。

先对输入做层归一化，再进入多头注意力层，捕捉 token 间关系，随后用残差连接把结果加回原向量；
再做一次层归一化，送入逐位置前馈网络（先扩维再缩维，中间用 GELU），同样用残差连接；
两处子层内部都配有 Dropout 防止过拟合。层归一化稳定分布，残差连接缓解梯度消失并保留恒等路径。

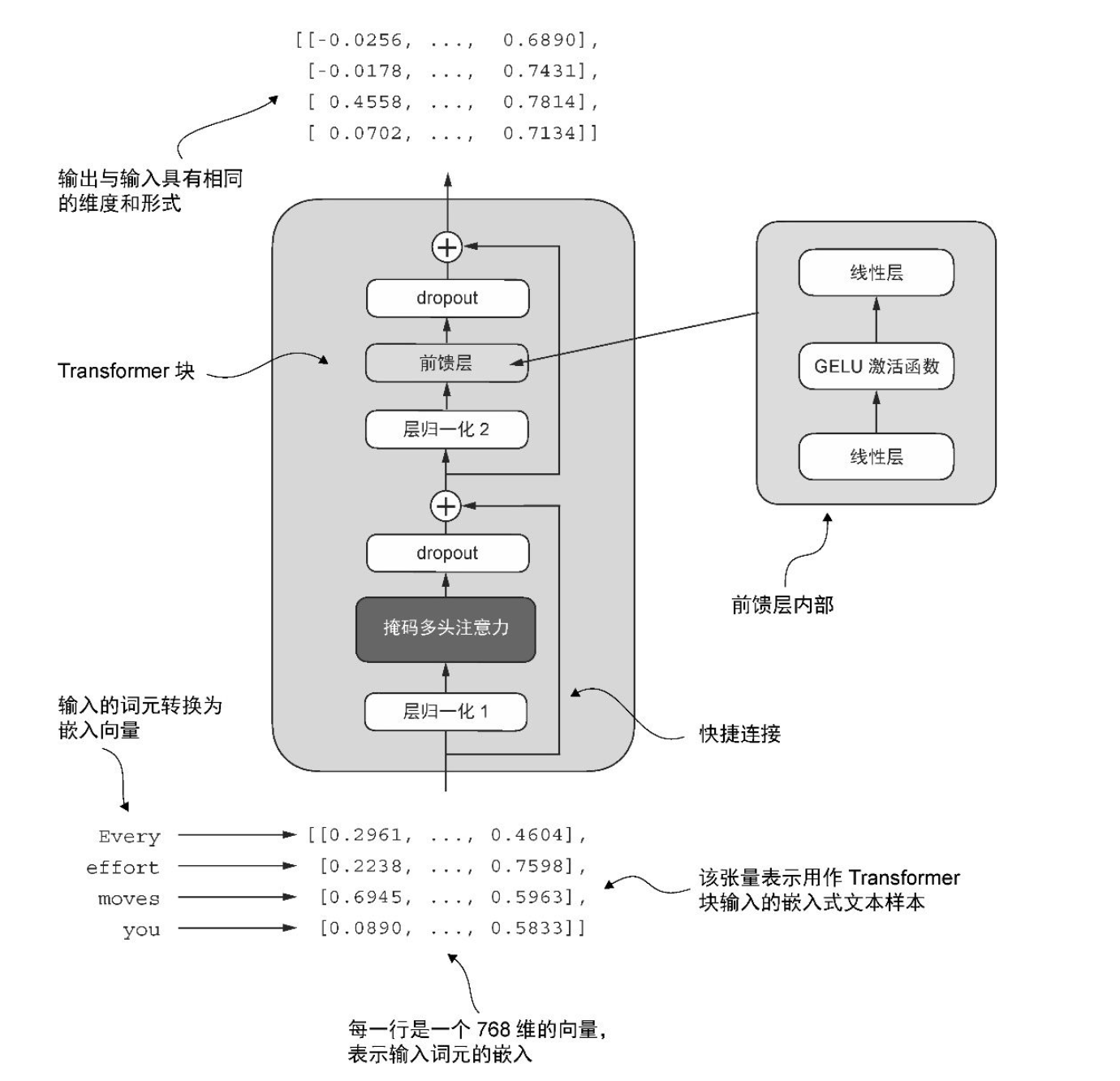
图源于《从零构建大模型》

代码解释：

前层归一化（Pre-LayerNorm）和后层归一化(Post-LayerNorm)
Transformer块让输入和输出保持不变，为什么？这种设计使其能有效应用于各种序列到序列的任务，其中每个输出向量直接对应一个输入向量，保持一一对应的关系。

from attention_mechanism.attention_module import MultiHeadAttention
class TransformerBlock(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()
        self.attention = MultiHeadAttention(
            d_in = config["emb_dim"],
            d_out = config["emb_dim"],
            context_length = config["context_length"],
            dropout = config["drop_rate"],
            num_heads = config["n_heads"],
            qkv_bias = config["qkv_bias"]
        )

        self.ff = FeedForward(config)
        self.norm1 = LayerNorm(config["emb_dim"])
        self.norm2 = LayerNorm(config["emb_dim"])
        self.dropout = nn.Dropout(config["drop_rate"])
    def forward(self, x):
        shortcut = x
        x = self.norm1(x)
        x = self.attention(x)
        x = self.dropout(x) 
        x = x + shortcut

        shortcut = x
        x = self.norm2(x)
        x = self.ff(x)
        x = self.dropout(x)
        x = x + shortcut

        return x

六、GPT架构的真正实现

GPT大语言模型的组件包括嵌入层、Transformer块和输出层。

嵌入层：输入序列首先被转换成词元嵌入，然后用位置嵌入进行增强。

Transformer块：通过一系列Transformer块（每个块都包含多头注意力和前馈神经网络层，并带有dropout和层归一化功能），这些块相互堆叠并重复12次最终Transformer块的输出会经过最后一步的层归一化处理，然后传递到线性输出层。

输出层：将Transformer的输出映射到一个高维空间（大小为对应模型的词汇表大小），以预测序列中的下一个词元。

class GPTModel(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()

        self.tok_emb = nn.Embedding(config["vocab_size"], config["emb_dim"])
        self.pos_emb = nn.Embedding(config["context_length"], config["emb_dim"])
        self.drop = nn.Dropout(config["drop_rate"])

        self.transformer_blocks = nn.Sequential(*[
            TransformerBlock(config) for _ in range(config["n_layers"])
        ])  # 使用占位符替换TransformerBlock

        self.final_norm = LayerNorm(config["emb_dim"])
        self.out_head = nn.Linear(config["emb_dim"], config["vocab_size"], bias=False)

    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_emb = self.tok_emb(in_idx)
        pos_emb = self.pos_emb(torch.arange(seq_len, device=in_idx.device))
        
        x = tok_emb + pos_emb
        x = self.drop(x)
        x = self.transformer_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

七、GPT将输出张量转为文本

做法：模型在每轮迭代中预测下一个词元，并将其添加到输入上下文中以进行下一轮预测
步骤：
细节：在每一步中，模型输出一个矩阵，其中的向量表示有可能的下一个词元。将与下一个词元对应的向量提取出来，并通过softmax函数转换为概率分布。在包含这些概率分数的向量中，找到最高值的索引，这个索引对应于词元ID。然后将这个词元ID解码为文本，生成序列中的下一个词元。最后，将这个词元附加到之前的输入中，形成新的输入序列，供下一次迭代使用。这个逐步的过程使得模型能够按顺序生成文本，从最初的输入上下文中构建连贯的短语和句子。

代码解读

贪心解码每一步都只选概率最高的词模型输出一个词汇表大小的概率分布后，直接取 argmax 得到当前最可能的 token，然后把它作为下一步的输入，再继续预测，直到遇到结束符或达到最大长度。
idx[:, -context_size:] 的作用是：只保留每个样本（batch 中的每一行）最后的 context_size 个 token。
-context_size: 表示从倒数第 context_size 个元素开始，一直取到末尾。

def generate_text_simple(model, idx, max_new_tokens, context_size):
    for _ in range(max_new_tokens):
        # 将当前文本截断至大模型支持的长度
        idx_cond = idx[:, -context_size:]
        with torch.no_grad():
            logits = model(idx_cond)
        # 仅关注最后一个时间步的logits
        logits = logits[:, -1, :]
        # 转换为概率分布
        probs = torch.softmax(logits, dim=-1)
        # 采样下一个token
        idx_next = torch.argmax(probs, dim=-1, keepdim=True)
        # 拼接采样的token
        idx = torch.cat((idx, idx_next), dim=1)
    return idx

尝试输入 “Hello, I am a robot.”

输出结果为 ”Hello, I am a robot.mail unheard lawn nan Mac bridinates spring denotesnosis” 。

model.eval()
    out = generate_text_simple(
        model, 
        batch, 
        max_new_tokens=10, 
        context_size=GPT_CONFIG_124M["context_length"])

到目前为止，我们只是实现了GPT架构，并用初始随机权重初始化了GPT模型实例，并没有对其训练，所以输出的是无意义的文本。

八、了解模型架构及其规模

权重共享

用文章最前面初始化的GPT_CONFIG_124M（1.24亿）初始化模型，并计算构造的GPT的参数量，发现实际的参数量是1.63亿。

# 通过numel()（“number of elements”的缩写）方法统计模型参数张量的总参数量
model = GPTModel(GPT_CONFIG_124M)

total_params = sum(p.numel() for p in model.parameters())
    print(f"Total number of parameters: {total_params:,}")
    
# Total number of parameters: 163,009,536

那这个差距是怎么来的呢？

因为原始的GPT-2的架构中使用了“权重共享”——输出层的权重矩阵直接复用词元嵌入层的权重。

词元嵌入层和线性输出层的权重具有相同的形状，都是[50257, 768]（总参数量词表大小 V = 50 257，嵌入层维度 d = 768）。这两层的大小为50 257 × 768 ≈ 38.6 M。

1.63亿- 0.386亿= 1.24亿。

前馈模块和注意力模块包含的参数量

已知 GPT-2 (small) 超参
d_model = 768
d_ff = 4 × d_model = 3072
n_head = 12
vocab_size = 50257（只影响嵌入/输出层，不影响 block 内部）

FeedForward: 4,722,432

FeedForward（两层全连接)

权重矩阵形状
W₁: d_model × d_ff = 768 × 3072
b₁: 3072
W₂: d_ff × d_model = 3072 × 768
b₂: 768

参数量 = 768×3072 + 3072 + 3072×768 + 768
= 2×(768×3072) + 3072 + 768
= 4,718,592 + 3,072 + 768
= 4,722,432

MultiHeadAttention：2,361,600

MultiHeadAttention（含 4 个线性映射：Q, K, V, O）
每个 head 的 d_head = 768 / 12 = 64
四个权重矩阵形状都是 d_model × d_model = 768 × 768，没有额外偏置。
参数量 = 4 × (768×768)
= 4 × 589,824
= 2,359,296
但 PyTorch 的 nn.MultiheadAttention 实现里默认 给 QKV 加偏置，而 O 投影无偏置：
3 个偏置 (768 维) = 3 × 768 = 2,304
因此实际计算常看到 2,359,296 + 2,304 = 2,361,600。

内存需求 GPTModel对象中1.63亿个参数的内存需求，并假设每个参数是占用4字节的32位浮点数。

total_size_bytes = total_params * 4  # 32微浮点数
total_size_mb = total_size_bytes / 1024 / 1024  # 转为兆字节
print(f"Total size: {total_size_mb:.2f} MB")

模型需要的内存空间为621.83 MB。