2023-12-07 Kernel Function 核函数

发布于 2023年12月07日 • 2 分钟 • 981 字

Table of contents

1. 正态分布的表示
2. 核函数是什么，有什么类型
3. 已知先验知识，如何计算后验分布

这篇文章主要解决三个问题：

正态分布的表示
核函数是什么，有什么类型
已知先验知识，如何计算后验分布

1. 正态分布的表示

正态分布一般表示为$f \sim N(0,K)$，书上写作 $p(f|x) = N(f|0,K)$。

为啥要多写一个f呢？

因为这个分布是针对f的分布，换句话说这里的随机变量是f，再换句话就是说这个随机变量f遵守一个正态分布。

2. 核函数是什么，有什么类型

核函数就是协方差。

核函数$K(x_i, x_j)$

它计算在输入空间中任意两个点的相似度，可以用欧式距离表示。
它度量输入空间中两点$x_i$和$x_j$之间的统计关系。
它量化$x_j$的变化和$x_i$的相应变化之间的相关性。

选择不同核函数，表示数据点之间的相关性被用不同方式来衡量。

有几种常见的核：

高斯核 Gaussian kernel

1.1 常见的高斯核

$$ K_{ij} = k(x_i,x_j) = e^{-||X_i-X_j||^2}$$

这里把负平方距离的指数作为距离度量。当x_i和x_j距离非常远，我们有x_i-x_j 趋向于无穷大，此时k_{ij}趋向于0。当x_i和x_j相等，k_{ij}等于1。K是一个介于0和1之间的数，由此就可以表现点之间的相关性。

1.2 可调节参数的高斯核，又被叫做isotropic squared exponential kernel

$$K_{ij} = k(x_i,x_j) = \sigma_f^2e^{-\frac{1}{2l^2}||X_i-X_j||^2}$$ 2. 略(以后补充，暂时不是重点)

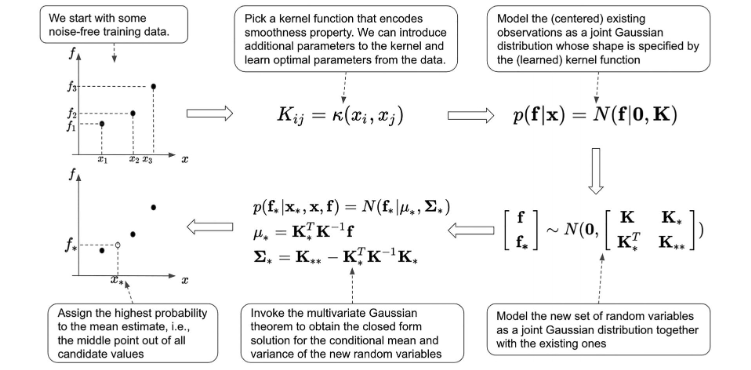
3. 已知先验知识，如何计算后验分布

假设我们有三个无噪声观测值，$ D = {(x_1,f(x_1)), (x_2, f(x_2)),(x_3, f(x_3))}$。我们需要对这三个随机变量进行建模。假设mean vector 为 $\mu$， covariance matrix为$K$。

这三个变量遵循多元变量的高斯分布

$\\bold f = \\begin{bmatrix}\nf(x_1) \\f(x_2) \\f(x_3) \\end{bmatrix} \\sim N(\\mu, K) =N(\\begin{bmatrix}\n0 \\0 \\0\\end{bmatrix} ,\\begin{bmatrix}\nk_{11}&k_{12}&k_{13} \\k_{21}&k_{22}&k_{23}\\k_{31}&k_{32}&k_{33}\\end{bmatrix})$

基于这个数据集D，假设我们现在想知道另一个变量$x_4$（它对应的f值用$f_*(x_4)$表示）在其他位置的均值和方差的的分布。

问题：f 和f* 是同一个分布吗？不是，用不同的字母表示不同的分布。

f和f*的分布为

$\\bold f \\sim N(0,K)$

$\\bold f_* \\sim N(0,k(x_4,x_4))$

如何求这个后验概率呢？

我们可以将观察到的数据集与新变量一起构造一个联合分布。

我们已经知道，数据集D最的观测值f和f(x_4)分别遵循分布

$\\bold f \\sim N(0,K)$

$f(x_4) \\sim N(0, k(x_4,x_4)) = N(0,1)$

假设四个数据的建模为随机变量$f_{new}$

$\\bold f_{new} = \\begin{bmatrix}\nf(x_1) \\f(x_2) \\f(x_3) \\f_*(x_4) \\end{bmatrix} \\sim N(\\mu, K) =N(\\begin{bmatrix}\n0 \\0 \\0\\0\\end{bmatrix} ,\\begin{bmatrix}\nk_{11}&k_{12}&k_{13} &k_{14} \\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\end{bmatrix}) \\sim N(0,\\begin{bmatrix}\nK &K_{4}\\K_{4}^T&K_{44}\\end{bmatrix})$